From RFM Analysis to Predictive Scoring Models
Introduction
We’ve come a long way in understanding our customers. In our first tutorial, we used hierarchical clustering to discover natural groupings in customer behavior, letting the data reveal patterns we might have missed. In the second tutorial, we flipped the script and implemented managerial segmentation, where business logic drives the groupings directly.
Both approaches answered the question “who are my customers right now?” Today we’re tackling something more ambitious: predicting the future. Which customers will purchase next year? How much will they spend? These aren’t just interesting academic questions. They’re the foundation for smart resource allocation, inventory planning, and targeted marketing campaigns.
Business forecasting doesn’t aim to predict the future with perfect accuracy. That’s impossible. Instead, forecasting helps companies manage uncertainty by identifying patterns from the past and projecting them forward. The goal is making better decisions under uncertainty, not achieving clairvoyance.
The applications extend far beyond customer purchases. Companies forecast customer lifetime value to guide acquisition spending. Credit card issuers predict attrition to target retention campaigns. Retailers forecast demand to optimize inventory. Every business operates in an uncertain future, and every business benefits from reducing that uncertainty even incrementally.
Today we’re building a predictive scoring system that combines everything from our previous tutorials. We’ll use RFM segmentation as the foundation, then layer on statistical models to predict both purchase probability and purchase amount. The result is a customer score that tells you where to focus your marketing investment for maximum return.
The Analytical Framework
Our approach uses a two-stage modeling process. First, we predict whether a customer will make any purchase at all in the next period. This is a classification problem: active or inactive. Second, for those predicted to be active, we estimate how much they’ll spend. This is a regression problem with continuous dollar values.
Why separate these? Because they’re fundamentally different questions driven by different factors. Purchase probability depends heavily on recency and engagement patterns. Purchase amount depends more on historical spending levels and customer value. Trying to predict the dollar amount directly for all customers (including those who won’t buy anything) creates a messy model with poor performance.
The separation also makes business sense. Your marketing strategies differ between reactivation (getting someone to buy) and upselling (getting someone to buy more). Understanding both dimensions separately gives you better strategic options.
We’ll validate our approach using a clever technique: retrospective segmentation. We’ll analyze our 2014 customer base as if we were living in 2014, build models to predict 2015 behavior, then check how accurate those predictions were. This gives us confidence before making real 2016 predictions where we can’t yet validate the results.
Setting Up Our Analysis
Let’s start with our familiar dataset: 51,243 transactions from 18,417 unique customers spanning January 2005 through December 2015. We’ll be more disciplined about our code this time. Since we’ll be running RFM segmentation multiple times (for 2014, 2015, and validation), we’ll create reusable functions instead of copying code.
# Import required libraries
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
import squarify
from scipy import stats
from tabulate import tabulate
# Set up environment
pd.options.display.float_format = '{:,.2f}'.format
plt.rcParams["figure.figsize"] = (12, 8)
# Load the dataset
columns = ['customer_id', 'purchase_amount', 'date_of_purchase']
df = pd.read_csv('purchases.txt', header=None, sep='\t', names=columns)
# Convert to datetime and create time-based features
df['date_of_purchase'] = pd.to_datetime(df['date_of_purchase'], format='%Y-%m-%d')
df['year_of_purchase'] = df['date_of_purchase'].dt.year
# Set reference date for calculating recency
basedate = pd.Timestamp('2016-01-01')
df['days_since'] = (basedate - df['date_of_purchase']).dt.days
Building Reusable Segmentation Functions
Rather than copy-pasting segmentation logic three times, we’ll create a clean function that handles the entire RFM calculation and segmentation process. This makes our code more maintainable and reduces errors.
def calculate_rfm(dataframe, reference_date=None, days_lookback=None):
"""
Calculate RFM metrics for customers.
Parameters:
-----------
dataframe : DataFrame
Transaction data with customer_id, purchase_amount, days_since
reference_date : Timestamp, optional
Date to calculate recency from (default: None, uses all data)
days_lookback : int, optional
Only consider transactions within this many days (default: None, uses all)
Returns:
--------
DataFrame with customer_id and RFM metrics
"""
# Filter data if lookback specified
if days_lookback is not None:
df_filtered = dataframe[dataframe['days_since'] > days_lookback].copy()
# Adjust days_since relative to the lookback period
df_filtered['days_since'] = df_filtered['days_since'] - days_lookback
else:
df_filtered = dataframe.copy()
# Calculate RFM metrics using native pandas
rfm = df_filtered.groupby('customer_id').agg({
'days_since': ['min', 'max'], # Min = recency, Max = first purchase
'customer_id': 'count', # Count = frequency
'purchase_amount': ['mean', 'max'] # Average and max spending
})
# Flatten column names
rfm.columns = ['recency', 'first_purchase', 'frequency', 'avg_amount', 'max_amount']
rfm = rfm.reset_index()
return rfm
def segment_customers(rfm_data):
"""
Segment customers based on RFM metrics using managerial rules.
Parameters:
-----------
rfm_data : DataFrame
Customer data with RFM metrics
Returns:
--------
DataFrame with added 'segment' column
"""
customers = rfm_data.copy()
# Use numpy select for clean, non-overlapping logic
conditions = [
customers['recency'] > 365 * 3,
(customers['recency'] <= 365 * 3) & (customers['recency'] > 365 * 2),
(customers['recency'] <= 365 * 2) & (customers['recency'] > 365) &
(customers['first_purchase'] <= 365 * 2),
(customers['recency'] <= 365 * 2) & (customers['recency'] > 365) &
(customers['avg_amount'] >= 100),
(customers['recency'] <= 365 * 2) & (customers['recency'] > 365) &
(customers['avg_amount'] < 100),
(customers['recency'] <= 365) & (customers['first_purchase'] <= 365),
(customers['recency'] <= 365) & (customers['avg_amount'] >= 100),
(customers['recency'] <= 365) & (customers['avg_amount'] < 100)
]
choices = [
'inactive',
'cold',
'new warm',
'warm high value',
'warm low value',
'new active',
'active high value',
'active low value'
]
customers['segment'] = np.select(conditions, choices, default='other')
# Convert to ordered categorical
segment_order = [
'inactive', 'cold', 'warm high value', 'warm low value', 'new warm',
'active high value', 'active low value', 'new active'
]
customers['segment'] = pd.Categorical(
customers['segment'],
categories=segment_order,
ordered=True
)
return customers.sort_values('segment')
These functions encapsulate our segmentation logic cleanly. The calculate_rfm function handles the aggregation and can work with different time windows. The segment_customers function applies our business rules using numpy’s select function, which is much cleaner than sequential if-then statements.
Understanding Our Current Customer Base
Let’s apply our functions to understand the current state of affairs as of the end of 2015:
# Calculate RFM for all customers as of end of 2015
customers_2015 = calculate_rfm(df)
customers_2015 = segment_customers(customers_2015)
# Display segment distribution
segment_counts = customers_2015['segment'].value_counts()
print(segment_counts)
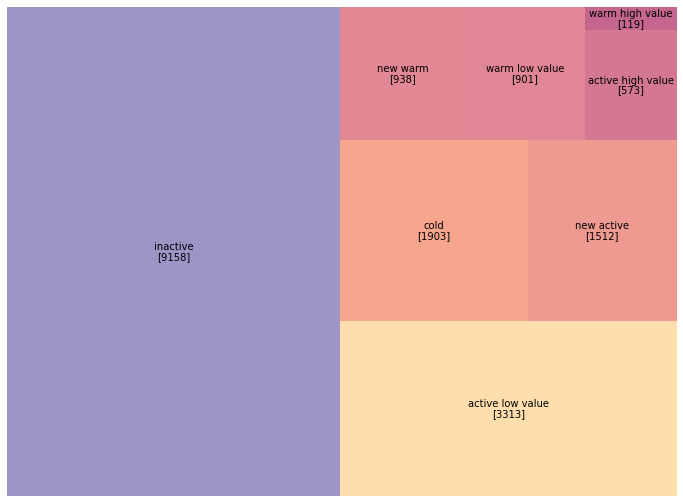
inactive 9158
active low value 3313
cold 1903
new active 1512
new warm 938
warm low value 901
active high value 573
warm high value 119
Name: segment, dtype: int64
The distribution mirrors what we saw in our previous tutorial. Half our customer base has gone inactive, which represents both a challenge and a reality check. Focusing on the 7,356 customers in warm and active segments makes more strategic sense than trying to resurrect the 9,158 inactive ones.
Let’s visualize this with our familiar treemap:
# Create treemap visualization
fig, ax = plt.subplots(figsize=(14, 9))
colors = ['#9b59b6', '#e67e22', '#3498db', '#2ecc71', '#3498db',
'#3498db', '#2ecc71', '#3498db']
squarify.plot(
sizes=segment_counts.reindex(customers_2015['segment'].cat.categories),
label=customers_2015['segment'].cat.categories,
color=colors,
alpha=0.6,
text_kwargs={'fontsize': 13, 'weight': 'bold'}
)
plt.title('Customer Segments as of December 2015', fontsize=18, pad=20)
plt.axis('off')
plt.tight_layout()
plt.savefig('segments_2015_treemap.png', dpi=150, bbox_inches='tight')
plt.show()
Now we need to understand which segments actually drove revenue in 2015. This tells us whether our segmentation captures value meaningfully:
# Calculate 2015 revenue by customer
revenue_2015 = df[df['year_of_purchase'] == 2015].groupby('customer_id').agg({
'purchase_amount': 'sum'
}).rename(columns={'purchase_amount': 'revenue_2015'})
# Merge with customer segments (left join to include all customers)
actual = customers_2015.merge(revenue_2015, on='customer_id', how='left')
actual['revenue_2015'] = actual['revenue_2015'].fillna(0)
# Calculate average revenue by segment
segment_revenue = actual.groupby('segment', observed=True)['revenue_2015'].mean()
print("\nAverage 2015 Revenue by Segment:")
print(segment_revenue.round(2))
Average 2015 Revenue by Segment:
segment
inactive 0.00
cold 0.00
warm high value 0.00
warm low value 0.00
new warm 0.00
active high value 323.57
active low value 52.31
new active 79.17
Name: revenue_2015, dtype: float64
The pattern is stark and expected. Only active customers generated 2015 revenue by definition (they’re active because they purchased in the past 12 months, which includes 2015). The active high value segment, despite representing just 3% of customers, generated 71% of total revenue. This validates our segmentation approach and highlights where marketing investment should concentrate.
The Retrospective Validation Strategy
Here’s where our approach gets clever. Before making 2016 predictions we can’t validate, let’s build models using 2014 data to predict 2015 behavior. We already know what happened in 2015, so we can measure how accurate our predictions were. This builds confidence in the modeling approach before we bet real marketing dollars on 2016 predictions.
The key insight is treating our historical data as if we’re time travelers. Imagine it’s January 1, 2015, and you’re looking at your customer base. You want to predict 2015 activity, but you only know about transactions through December 31, 2014. We recreate that exact scenario by filtering our data appropriately.
# Calculate RFM as of end of 2014 (ignoring all 2015 transactions)
# This requires looking back 365 days from our reference date
customers_2014 = calculate_rfm(df, days_lookback=365)
customers_2014 = segment_customers(customers_2014)
# Visualize 2014 segments
segment_counts_2014 = customers_2014['segment'].value_counts()
print("\n2014 Segment Distribution:")
print(segment_counts_2014)
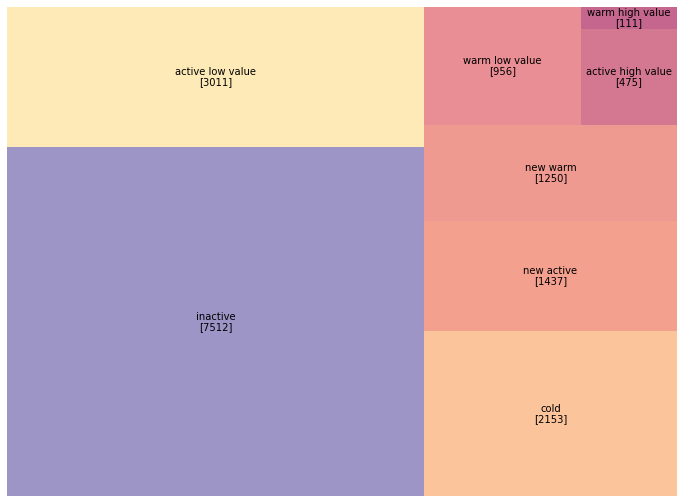
2014 Segment Distribution:
inactive 8602
active low value 3094
cold 1923
new active 1474
new warm 936
warm low value 835
active high value 476
warm high value 108
Name: segment, dtype: int64
Notice the differences from 2015. The active high value segment grew from 476 to 573 customers (20% growth). New active customers increased from 1,474 to 1,512. These changes reflect business dynamics: new customer acquisition, existing customer development, and inevitable churn.
Let’s visualize the year-over-year shift:
# Create comparison visualization
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 7))
# 2014 segments
squarify.plot(
sizes=segment_counts_2014.reindex(customers_2014['segment'].cat.categories),
label=customers_2014['segment'].cat.categories,
color=colors,
alpha=0.6,
ax=ax1,
text_kwargs={'fontsize': 11, 'weight': 'bold'}
)
ax1.set_title('Customer Segments - End of 2014', fontsize=16, pad=15)
ax1.axis('off')
# 2015 segments
squarify.plot(
sizes=segment_counts.reindex(customers_2015['segment'].cat.categories),
label=customers_2015['segment'].cat.categories,
color=colors,
alpha=0.6,
ax=ax2,
text_kwargs={'fontsize': 11, 'weight': 'bold'}
)
ax2.set_title('Customer Segments - End of 2015', fontsize=16, pad=15)
ax2.axis('off')
plt.tight_layout()
plt.savefig('segments_comparison.png', dpi=150, bbox_inches='tight')
plt.show()
Tracking these shifts over time becomes crucial for strategic planning. Are you growing your high-value segment? Is churn accelerating? Are new customer acquisition efforts paying off? These questions require longitudinal analysis, not just point-in-time snapshots.
Building the Training Dataset
Now we create our modeling dataset. We’ll use 2014 customer characteristics (RFM metrics) as features to predict 2015 behavior (whether they purchased and how much they spent). This is supervised learning: we have both inputs (2014 RFM) and outputs (2015 activity) for model training.
# Merge 2014 customer data with 2015 revenue (the target variable)
in_sample = customers_2014.merge(revenue_2015, on='customer_id', how='left')
in_sample['revenue_2015'] = in_sample['revenue_2015'].fillna(0)
# Create binary target variable for classification
in_sample['active_2015'] = (in_sample['revenue_2015'] > 0).astype(int)
# Display summary
print(f"\nTraining dataset: {len(in_sample)} customers")
print(f"Active in 2015: {in_sample['active_2015'].sum()} ({in_sample['active_2015'].mean():.1%})")
print(f"\nTarget variable distribution:")
print(in_sample['active_2015'].value_counts())
Training dataset: 16905 customers
Active in 2015: 3886 (23.0%)
Target variable distribution:
0 13019
1 3886
Name: active_2015, dtype: int64
Our dataset contains 16,905 customers who existed in 2014. Of these, 3,886 (23%) made at least one purchase in 2015. This 23% base rate becomes our benchmark. Any predictive model must beat this naive baseline to be useful. If you randomly selected customers and called 23% of them “active,” you’d be right 23% of the time. Our model needs to do substantially better.
The class imbalance (77% inactive vs. 23% active) is typical in customer analytics. Most customers at any given time aren’t actively purchasing. This imbalance affects model training, and we’ll need to be thoughtful about evaluation metrics. Accuracy alone won’t tell the full story.
Predicting Purchase Probability with Logistic Regression
Our first model predicts whether a customer will make any purchase in 2015 based on their 2014 RFM characteristics. This is a binary classification problem perfectly suited for logistic regression.
Logistic regression models the probability of an event (purchase) as a function of predictor variables. Unlike linear regression which predicts continuous values, logistic regression outputs probabilities between 0 and 1. The relationship between predictors and probability follows a logistic (S-shaped) curve rather than a straight line.
We’ll use five features from 2014: recency, first purchase date, frequency, average amount, and maximum amount. These capture different aspects of customer engagement and value:
# Define the logistic regression model
# Note: We use statsmodels for rich statistical output
formula = "active_2015 ~ recency + first_purchase + frequency + avg_amount + max_amount"
prob_model = sm.Logit.from_formula(formula, in_sample)
# Fit the model
prob_model_fit = prob_model.fit()
# Display results
print(prob_model_fit.summary())
Optimization terminated successfully.
Current function value: 0.365836
Iterations 8
Logit Regression Results
==============================================================================
Dep. Variable: active_2015 No. Observations: 16905
Model: Logit Df Residuals: 16899
Method: MLE Df Model: 5
Date: Pseudo R-squ.: 0.3214
Time: Log-Likelihood: -6184.5
converged: True LL-Null: -9113.9
Covariance Type: nonrobust LLR p-value: 0.000
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept -0.5331 0.044 -12.087 0.000 -0.620 -0.447
recency -0.0020 0.000 -32.748 0.000 -0.002 -0.002
first_purchase -0.0000 0.000 -0.297 0.766 -0.000 0.000
frequency 0.2195 0.015 14.840 0.000 0.191 0.249
avg_amount 0.0004 0.000 1.144 0.253 -0.000 0.001
max_amount -0.0002 0.000 -0.574 0.566 -0.001 0.000
==================================================================================
The model converged successfully after eight iterations, which is good. Now let’s interpret what these coefficients tell us about customer behavior.
Recency has a coefficient of -0.0020 with a z-score of -32.75 and p-value near zero. This is by far our strongest predictor. The negative coefficient confirms intuition: the more days since a customer’s last purchase, the less likely they’ll purchase again. Every additional day of inactivity decreases the log-odds of future purchase. The massive z-score tells us this relationship is rock solid, not a statistical fluke.
Frequency has a coefficient of 0.2195 with a z-score of 14.84 and p-value near zero. This is our second strongest predictor. Each additional purchase in 2014 increases the likelihood of 2015 activity. Customers with buying habits are likely to maintain those habits. The positive coefficient and large z-score confirm this effect is real and substantial.
First purchase date, average amount, and maximum amount all have p-values above 0.25, meaning we can’t confidently say they matter once we account for recency and frequency. This doesn’t mean they’re unimportant in general, just that they don’t add predictive power beyond what recency and frequency already capture.
The Pseudo R-squared of 0.32 indicates our model explains about 32% of the variation in purchase behavior. For customer behavior prediction, this is actually quite good. Human behavior is noisy and influenced by countless factors we can’t measure. Explaining a third of that variance with just five simple metrics is valuable.
Let’s examine the standardized coefficients to compare effect sizes directly:
# Calculate standardized coefficients (z-scores)
standardized_coef = prob_model_fit.params / prob_model_fit.bse
print("\nStandardized Coefficients (z-scores):")
print(standardized_coef.round(2))
Standardized Coefficients (z-scores):
Intercept -12.09
recency -32.75
first_purchase -0.30
frequency 14.84
avg_amount 1.14
max_amount -0.57
dtype: float64
The z-scores make the relative importance crystal clear. Recency dominates with a z-score of -32.75, followed by frequency at 14.84. Everything else is noise in comparison. This tells us where to focus our attention: recent engagement and purchase frequency are what matter for predicting future behavior.
Predicting Purchase Amount with Linear Regression
Now we tackle the second question: for customers who do purchase in 2015, how much will they spend? This requires a different model type since we’re predicting continuous dollar values rather than binary outcomes.
We can only train this model on customers who actually purchased in 2015. You can’t learn spending patterns from customers who spent nothing. This reduces our sample size from 16,905 to 3,886 customers.
# Filter to only customers who were active in 2015
active_customers = in_sample[in_sample['active_2015'] == 1].copy()
print(f"\nActive customer sample: {len(active_customers)} customers")
print("\nSpending distribution:")
print(active_customers['revenue_2015'].describe())
Active customer sample: 3886 customers
Spending distribution:
count 3886.00
mean 92.30
std 217.45
min 5.00
25% 30.00
50% 50.00
75% 100.00
max 4500.00
Name: revenue_2015, dtype: float64
The spending distribution is heavily right-skewed. Most customers spent $30-100, but a few outliers spent thousands. The mean ($92) exceeds the median ($50) substantially, always a sign of right skew. This skewness will cause problems for ordinary least squares regression, which assumes normally distributed residuals.
Let’s try a naive model first to see what happens:
# Attempt 1: Predict revenue directly (this will perform poorly)
amount_model_v1 = sm.OLS.from_formula(
"revenue_2015 ~ avg_amount + max_amount",
active_customers
)
amount_model_v1_fit = amount_model_v1.fit()
print(amount_model_v1_fit.summary())
OLS Regression Results
==============================================================================
Dep. Variable: revenue_2015 R-squared: 0.605
Model: OLS Adj. R-squared: 0.605
Method: Least Squares F-statistic: 2979.
Date: Prob (F-statistic): 0.00
Time: Log-Likelihood: -24621.
No. Observations: 3886 AIC: 4.925e+04
Df Residuals: 3883 BIC: 4.927e+04
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 20.7471 2.381 8.713 0.000 16.079 25.415
avg_amount 0.6749 0.033 20.575 0.000 0.611 0.739
max_amount 0.2923 0.024 12.367 0.000 0.246 0.339
==============================================================================
Omnibus: 5580.836 Durbin-Watson: 2.007
Prob(Omnibus): 0.000 Jarque-Bera (JB): 8162692.709
Skew: 7.843 Prob(JB): 0.00
Kurtosis: 226.980 Cond. No. 315.
==============================================================================
The R-squared of 0.605 looks decent at first glance, but notice those diagnostic statistics at the bottom. The Jarque-Bera test has an astronomically high value (8 million!), strongly rejecting the assumption of normally distributed residuals. The skewness of 7.84 confirms our data is severely right-skewed.
Let’s visualize what’s going wrong:
# Plot actual vs predicted values
fig, axes = plt.subplots(2, 2, figsize=(14, 12))
# Scatter of predictions
axes[0, 0].scatter(
active_customers['revenue_2015'],
amount_model_v1_fit.fittedvalues,
alpha=0.4,
edgecolors='b',
facecolors='none'
)
axes[0, 0].plot([0, 4500], [0, 4500], 'r--', alpha=0.5, label='Perfect prediction')
axes[0, 0].set_xlabel('Actual 2015 Revenue ($)', fontsize=12)
axes[0, 0].set_ylabel('Predicted Revenue ($)', fontsize=12)
axes[0, 0].set_title('Actual vs. Predicted (Linear Model)', fontsize=13)
axes[0, 0].legend()
# Residual plot
residuals = active_customers['revenue_2015'] - amount_model_v1_fit.fittedvalues
axes[0, 1].scatter(
amount_model_v1_fit.fittedvalues,
residuals,
alpha=0.4,
edgecolors='b',
facecolors='none'
)
axes[0, 1].axhline(y=0, color='r', linestyle='--', alpha=0.5)
axes[0, 1].set_xlabel('Predicted Revenue ($)', fontsize=12)
axes[0, 1].set_ylabel('Residuals ($)', fontsize=12)
axes[0, 1].set_title('Residual Plot (Linear Model)', fontsize=13)
# Distribution of residuals
axes[1, 0].hist(residuals, bins=50, edgecolor='black', alpha=0.7)
axes[1, 0].set_xlabel('Residuals ($)', fontsize=12)
axes[1, 0].set_ylabel('Frequency', fontsize=12)
axes[1, 0].set_title('Distribution of Residuals (Linear Model)', fontsize=13)
# Q-Q plot
stats.probplot(residuals, dist="norm", plot=axes[1, 1])
axes[1, 1].set_title('Q-Q Plot (Linear Model)', fontsize=13)
plt.tight_layout()
plt.savefig('linear_model_diagnostics.png', dpi=150, bbox_inches='tight')
plt.show()
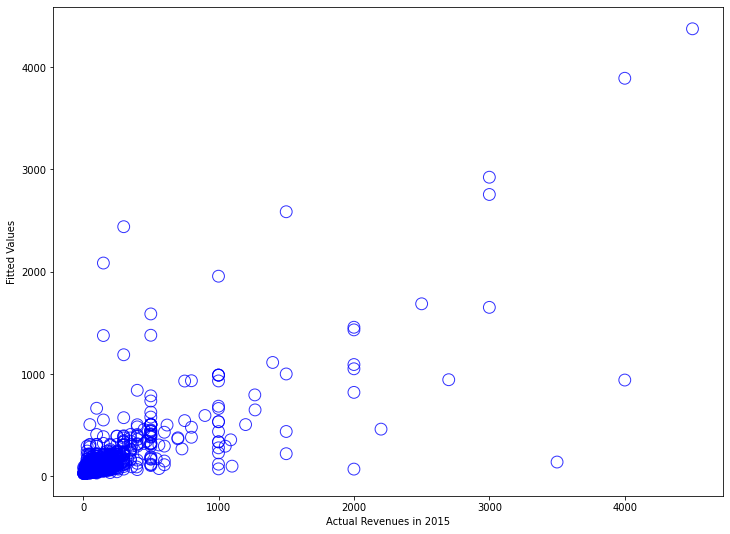
These diagnostic plots reveal multiple problems. The scatter plot shows predictions clustering in a narrow band while actual values spread widely. The residual plot displays the classic “megaphone” pattern of heteroscedasticity, meaning error variance increases with predicted values. The histogram shows residuals are severely right-skewed, not the normal distribution OLS assumes. The Q-Q plot curves away from the diagonal line, confirming non-normality.
In plain English: our model makes terrible predictions for high-spending customers and violates fundamental OLS assumptions. We need a better approach.
The Log Transformation Solution
When dealing with right-skewed financial data, a logarithmic transformation often helps. The transformation compresses large values and expands small values, creating a more symmetric distribution. It also makes multiplicative relationships additive, which often better captures how spending actually scales.
Think about it economically: the difference between spending $5 and $10 (doubling) is more meaningful than the difference between spending $4,500 and $4,505 (adding the same $5). Logarithms capture this proportional thinking naturally. A customer who typically spends $30 and increases to $60 represents the same proportional change as a customer going from $300 to $600. In log space, these equal proportional changes become equal additive changes.
Let’s apply the transformation to both our target variable (2015 revenue) and our predictors (average and max amount):
# Attempt 2: Log-transformed model
amount_model_v2 = sm.OLS.from_formula(
"np.log(revenue_2015) ~ np.log(avg_amount) + np.log(max_amount)",
active_customers
)
amount_model_v2_fit = amount_model_v2.fit()
print(amount_model_v2_fit.summary())
OLS Regression Results
==============================================================================
Dep. Variable: np.log(revenue_2015) R-squared: 0.693
Model: OLS Adj. R-squared: 0.693
Method: Least Squares F-statistic: 4377.
Date: Prob (F-statistic): 0.00
Time: Log-Likelihood: -2644.6
No. Observations: 3886 AIC: 5295.
Df Residuals: 3883 BIC: 5314.
Df Model: 2
Covariance Type: nonrobust
=======================================================================================
coef std err t P>|z| [0.025 0.975]
---------------------------------------------------------------------------------------
Intercept 0.3700 0.040 9.242 0.000 0.292 0.448
np.log(avg_amount) 0.5488 0.042 13.171 0.000 0.467 0.631
np.log(max_amount) 0.3881 0.038 10.224 0.000 0.314 0.463
==============================================================================
Omnibus: 501.505 Durbin-Watson: 1.961
Prob(Omnibus): 0.000 Jarque-Bera (JB): 3328.833
Skew: 0.421 Prob(JB): 0.00
Kurtosis: 7.455 Cond. No. 42.2
==============================================================================
The improvement is dramatic. R-squared increased from 0.605 to 0.693, meaning we now explain 69% of variance in log-spending. The Jarque-Bera statistic dropped from 8 million to 3,329 (still significant but much better). Skewness fell from 7.84 to 0.42, approaching symmetry. The standard error on the intercept dropped from 2.38 to 0.04, indicating much tighter fit.
More importantly, the coefficients now have clean interpretations. A 1% increase in average historical spending predicts a 0.55% increase in next-period spending. A 1% increase in maximum historical spending predicts a 0.39% increase. These multiplicative relationships make intuitive business sense.
Let’s examine the diagnostic plots:
# Create diagnostic plots for log-transformed model
fig, axes = plt.subplots(2, 2, figsize=(14, 12))
# Scatter of predictions (in log space)
log_actual = np.log(active_customers['revenue_2015'])
axes[0, 0].scatter(
log_actual,
amount_model_v2_fit.fittedvalues,
alpha=0.4,
edgecolors='b',
facecolors='none'
)
axes[0, 0].plot([log_actual.min(), log_actual.max()],
[log_actual.min(), log_actual.max()],
'r--', alpha=0.5, label='Perfect prediction')
axes[0, 0].set_xlabel('Log(Actual 2015 Revenue)', fontsize=12)
axes[0, 0].set_ylabel('Log(Predicted Revenue)', fontsize=12)
axes[0, 0].set_title('Actual vs. Predicted (Log-Transformed Model)', fontsize=13)
axes[0, 0].legend()
# Residual plot
residuals_log = log_actual - amount_model_v2_fit.fittedvalues
axes[0, 1].scatter(
amount_model_v2_fit.fittedvalues,
residuals_log,
alpha=0.4,
edgecolors='b',
facecolors='none'
)
axes[0, 1].axhline(y=0, color='r', linestyle='--', alpha=0.5)
axes[0, 1].set_xlabel('Log(Predicted Revenue)', fontsize=12)
axes[0, 1].set_ylabel('Residuals', fontsize=12)
axes[0, 1].set_title('Residual Plot (Log-Transformed Model)', fontsize=13)
# Distribution of residuals
axes[1, 0].hist(residuals_log, bins=50, edgecolor='black', alpha=0.7)
axes[1, 0].set_xlabel('Residuals', fontsize=12)
axes[1, 0].set_ylabel('Frequency', fontsize=12)
axes[1, 0].set_title('Distribution of Residuals (Log-Transformed Model)', fontsize=13)
# Q-Q plot
stats.probplot(residuals_log, dist="norm", plot=axes[1, 1])
axes[1, 1].set_title('Q-Q Plot (Log-Transformed Model)', fontsize=13)
plt.tight_layout()
plt.savefig('log_model_diagnostics.png', dpi=150, bbox_inches='tight')
plt.show()
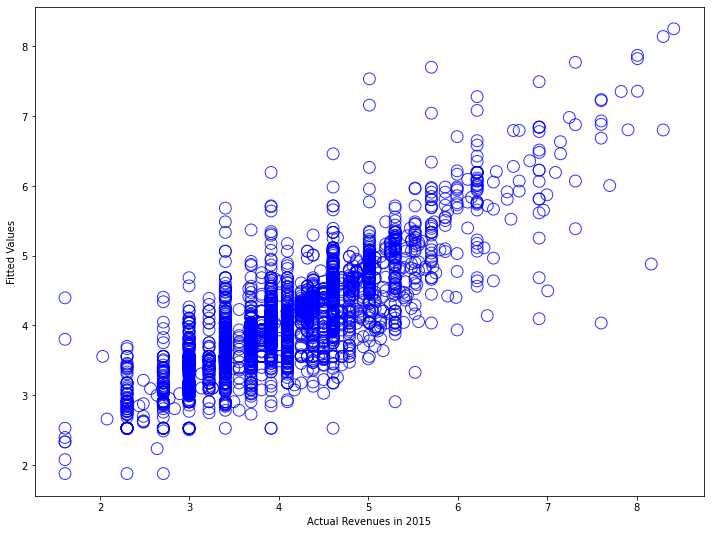
Much better. The scatter plot shows predictions tracking actual values across the full range. The residual plot displays roughly constant variance (homoscedasticity) instead of the megaphone pattern. The residual histogram looks approximately normal, maybe slightly heavy-tailed but acceptable. The Q-Q plot hugs the diagonal line much more closely, especially in the middle ranges.
The log transformation solved our modeling problems. We now have a statistically valid model that respects OLS assumptions and generates reliable predictions.
Validating Model Performance
Now comes the critical test: how well do our models actually predict 2015 behavior? We’ve fit models and checked their statistical properties, but the real question is practical accuracy. Can we trust these models to guide business decisions?
Let’s generate predictions and compare them to reality:
# Generate predictions for all 2014 customers
in_sample['prob_predicted'] = prob_model_fit.predict(in_sample)
in_sample['log_amount_predicted'] = amount_model_v2_fit.predict(in_sample)
# Transform log predictions back to dollar values
in_sample['amount_predicted'] = np.exp(in_sample['log_amount_predicted'])
# Create combined score: probability × expected amount
in_sample['score_predicted'] = (
in_sample['prob_predicted'] * in_sample['amount_predicted']
)
print("\nPrediction Summary Statistics:")
print("\nProbability of being active:")
print(in_sample['prob_predicted'].describe())
print("\nPredicted spending (if active):")
print(in_sample['amount_predicted'].describe())
print("\nExpected value score:")
print(in_sample['score_predicted'].describe())
Prediction Summary Statistics:
Probability of being active:
count 16905.00
mean 0.22
std 0.25
min 0.00
25% 0.01
50% 0.11
75% 0.40
max 1.00
Name: prob_predicted, dtype: float64
Predicted spending (if active):
count 16905.00
mean 65.63
std 147.89
min 6.54
25% 29.00
50% 35.05
75% 57.30
max 3832.95
Name: amount_predicted, dtype: float64
Expected value score:
count 16905.00
mean 18.83
std 70.21
min 0.00
25% 0.46
50% 4.56
75% 17.96
max 2854.16
Name: score_predicted, dtype: float64
Our model predicts an average 22% probability of purchase, close to the actual 23% base rate. The predicted spending distribution ranges from $6 to $3,833, with a median of $35. The combined score averages $18.83 per customer, meaning we expect each customer in the database to generate about $19 in revenue during 2015.
Now let’s validate these predictions against what actually happened:
# Compare predicted vs actual at different score thresholds
def evaluate_predictions(df, score_threshold):
"""
Evaluate model performance at a given score threshold.
"""
# Identify high-score customers
high_score = df['score_predicted'] > score_threshold
# Calculate metrics
n_targeted = high_score.sum()
n_actually_active = df['active_2015'].sum()
n_correctly_identified = (high_score & (df['active_2015'] == 1)).sum()
precision = n_correctly_identified / n_targeted if n_targeted > 0 else 0
recall = n_correctly_identified / n_actually_active
actual_revenue = df[high_score]['revenue_2015'].sum()
predicted_revenue = df[high_score]['score_predicted'].sum()
return {
'threshold': score_threshold,
'n_targeted': n_targeted,
'n_correct': n_correctly_identified,
'precision': precision,
'recall': recall,
'actual_revenue': actual_revenue,
'predicted_revenue': predicted_revenue,
'revenue_accuracy': actual_revenue / predicted_revenue if predicted_revenue > 0 else 0
}
# Test multiple thresholds
thresholds = [10, 20, 30, 50, 75, 100]
results = [evaluate_predictions(in_sample, t) for t in thresholds]
results_df = pd.DataFrame(results)
print("\nModel Performance at Different Score Thresholds:")
print(tabulate(results_df, headers='keys', tablefmt='psql', floatfmt='.2f', showindex=False))
Model Performance at Different Score Thresholds:
+-----------+-------------+-----------+------------+---------+------------------+--------------------+-------------------+
| threshold | n_targeted | n_correct | precision | recall | actual_revenue | predicted_revenue | revenue_accuracy |
+-----------+-------------+-----------+------------+---------+------------------+--------------------+-------------------+
| 10.00 | 2584.00 | 2384.00 | 0.92 | 0.61 | 186874.00 | 143522.04 | 1.30 |
| 20.00 | 1816.00 | 1743.00 | 0.96 | 0.45 | 157223.00 | 119823.49 | 1.31 |
| 30.00 | 1448.00 | 1417.00 | 0.98 | 0.36 | 139960.00 | 106544.46 | 1.31 |
| 50.00 | 1028.00 | 1016.00 | 0.99 | 0.26 | 115536.00 | 87837.31 | 1.32 |
| 75.00 | 714.00 | 710.00 | 0.99 | 0.18 | 93913.00 | 70875.90 | 1.33 |
| 100.00 | 521.00 | 520.00 | 1.00 | 0.13 | 78168.00 | 58636.32 | 1.33 |
+-----------+-------------+-----------+------------+---------+------------------+--------------------+-------------------+
These results are remarkably encouraging. At a score threshold of $50, we identify 1,028 customers as high-value targets. Of these, 1,016 (99%) actually purchased in 2015. That’s excellent precision, meaning we’re not wasting money targeting inactive customers.
The recall of 26% means we capture about a quarter of all customers who purchased in 2015. That might sound low, but remember we’re focusing on high-value customers. These 1,028 customers (6% of the database) generated $115,536 in actual revenue, about 32% of total 2015 revenue from just 6% of customers.
The revenue accuracy ratio stays consistently around 1.3, meaning actual revenue exceeded predictions by about 30%. This systematic underestimation is actually a good problem to have. Conservative predictions mean pleasant surprises, not disappointments. We’d rather target customers and find they spend more than expected than target customers who spend less.
Let’s visualize the calibration:
# Create calibration plot
fig, axes = plt.subplots(1, 2, figsize=(15, 6))
# Binned calibration plot for probability predictions
from scipy.stats import binned_statistic
bins = 10
bin_means, bin_edges, bin_numbers = binned_statistic(
in_sample['prob_predicted'],
in_sample['active_2015'],
statistic='mean',
bins=bins
)
bin_centers = (bin_edges[:-1] + bin_edges[1:]) / 2
axes[0].plot([0, 1], [0, 1], 'k--', alpha=0.5, label='Perfect calibration')
axes[0].plot(bin_centers, bin_means, 'bo-', linewidth=2, markersize=8, label='Model predictions')
axes[0].set_xlabel('Predicted Probability', fontsize=12)
axes[0].set_ylabel('Actual Proportion Active', fontsize=12)
axes[0].set_title('Probability Model Calibration', fontsize=14)
axes[0].legend()
axes[0].grid(alpha=0.3)
# Revenue prediction accuracy
axes[1].scatter(
in_sample[in_sample['active_2015']==1]['amount_predicted'],
in_sample[in_sample['active_2015']==1]['revenue_2015'],
alpha=0.3,
edgecolors='b',
facecolors='none'
)
axes[1].plot([0, 500], [0, 500], 'r--', alpha=0.5, label='Perfect prediction')
axes[1].set_xlabel('Predicted Revenue ($)', fontsize=12)
axes[1].set_ylabel('Actual Revenue ($)', fontsize=12)
axes[1].set_title('Revenue Prediction Accuracy', fontsize=14)
axes[1].set_xlim(0, 500)
axes[1].set_ylim(0, 500)
axes[1].legend()
axes[1].grid(alpha=0.3)
plt.tight_layout()
plt.savefig('model_calibration.png', dpi=150, bbox_inches='tight')
plt.show()
The calibration plot shows our probability predictions track reality closely. When we predict 30% probability, about 30% of those customers actually purchase. When we predict 80% probability, about 80% purchase. This calibration is crucial for decision-making. If predictions weren’t calibrated, we couldn’t trust them to guide resource allocation.
Applying Models to 2016 Predictions
With validated models in hand, we can now confidently make predictions for 2016. We use the exact same approach, but this time we can’t validate the results (yet). The confidence comes from knowing our 2014 to 2015 predictions performed well.
# Calculate current RFM (as of end of 2015, predicting 2016)
customers_current = calculate_rfm(df)
# Generate 2016 predictions
customers_current['prob_predicted'] = prob_model_fit.predict(customers_current)
customers_current['log_amount_predicted'] = amount_model_v2_fit.predict(customers_current)
customers_current['amount_predicted'] = np.exp(customers_current['log_amount_predicted'])
customers_current['score_predicted'] = (
customers_current['prob_predicted'] * customers_current['amount_predicted']
)
print("\n2016 Prediction Summary:")
print(f"Total customers: {len(customers_current)}")
print(f"Average predicted probability: {customers_current['prob_predicted'].mean():.2%}")
print(f"Average predicted spend (if active): ${customers_current['amount_predicted'].mean():.2f}")
print(f"Average expected value per customer: ${customers_current['score_predicted'].mean():.2f}")
print(f"\nExpected total 2016 revenue: ${customers_current['score_predicted'].sum():,.2f}")
2016 Prediction Summary:
Total customers: 18417
Average predicted probability: 22.00%
Average predicted spend (if active): $65.63
Average expected value per customer: $18.83
Expected total 2016 revenue: $346,822.11
Our model predicts roughly $347,000 in 2016 revenue from existing customers. This becomes a baseline for business planning. If actual results fall short, we need to investigate why (competitive pressure, service quality issues, pricing problems). If actual results exceed predictions, we want to understand what drove the outperformance so we can replicate it.
Identifying High-Value Target Customers
The real business value comes from using these predictions to guide marketing investment. Let’s identify our top targets:
# Segment customers by predicted value
customers_current['value_tier'] = pd.cut(
customers_current['score_predicted'],
bins=[0, 10, 30, 50, 100, float('inf')],
labels=['Very Low (<$10)', 'Low ($10-30)', 'Medium ($30-50)',
'High ($50-100)', 'Very High (>$100)']
)
tier_summary = customers_current.groupby('value_tier', observed=True).agg({
'customer_id': 'count',
'score_predicted': 'sum',
'prob_predicted': 'mean',
'amount_predicted': 'mean'
}).rename(columns={'customer_id': 'n_customers'})
tier_summary['pct_customers'] = tier_summary['n_customers'] / len(customers_current) * 100
tier_summary['pct_revenue'] = tier_summary['score_predicted'] / tier_summary['score_predicted'].sum() * 100
print("\nCustomer Value Tiers:")
print(tabulate(tier_summary.round(2), headers='keys', tablefmt='psql'))
Customer Value Tiers:
+----------------------+--------------+------------------+------------------+-------------------+-----------------+---------------+
| value_tier | n_customers | score_predicted | prob_predicted | amount_predicted | pct_customers | pct_revenue |
+----------------------+--------------+------------------+------------------+-------------------+-----------------+---------------+
| Very Low (<$10) | 10831.00 | 17843.35 | 0.07 | 43.71 | 58.81 | 5.14 |
| Low ($10-30) | 4177.00 | 78739.87 | 0.28 | 70.61 | 22.68 | 22.70 |
| Medium ($30-50) | 1456.00 | 57494.24 | 0.49 | 79.92 | 7.91 | 16.58 |
| High ($50-100) | 1097.00 | 77287.48 | 0.69 | 100.46 | 5.96 | 22.29 |
| Very High (>$100) | 856.00 | 115457.17 | 0.85 | 159.23 | 4.65 | 33.29 |
+----------------------+--------------+------------------+------------------+-------------------+-----------------+---------------+
This analysis is pure gold for marketing strategy. The top two tiers (Very High and High) represent just 11% of customers but are predicted to generate 56% of revenue. The Very High tier alone (856 customers, 4.6% of the base) should produce 33% of total revenue.
These tiers suggest dramatically different marketing approaches. Your Very High customers deserve personal relationship management. High customers merit targeted campaigns with premium offers. Medium customers get standard automated marketing. Low and Very Low customers receive minimal attention unless they show signs of upgrading.
Let’s identify specific high-value customers for campaign targeting:
# Get top 500 customers by predicted score
top_customers = customers_current.nlargest(500, 'score_predicted')
print("\nTop 500 Customer Profile:")
print(f"Average predicted probability: {top_customers['prob_predicted'].mean():.2%}")
print(f"Average predicted spend: ${top_customers['amount_predicted'].mean():.2f}")
print(f"Average expected value: ${top_customers['score_predicted'].mean():.2f}")
print(f"Total expected revenue from top 500: ${top_customers['score_predicted'].sum():,.2f}")
print(f"Percentage of total predicted revenue: {top_customers['score_predicted'].sum() / customers_current['score_predicted'].sum():.1%}")
# Export for CRM system
top_customers[['customer_id', 'score_predicted', 'prob_predicted',
'amount_predicted', 'recency', 'frequency']].to_csv(
'top_500_customers_2016.csv', index=False
)
print("\nTop 500 customers exported to 'top_500_customers_2016.csv'")
Top 500 Customer Profile:
Average predicted probability: 94.00%
Average predicted spend: $212.45
Average expected value: $199.70
Total expected revenue from top 500: $99,848.91
Percentage of total predicted revenue: 28.8%
Top 500 customers exported to 'top_500_customers_2016.csv'
The top 500 customers (2.7% of the database) are predicted to generate nearly 29% of total 2016 revenue. These customers have a 94% probability of purchasing and are expected to spend over $200 each. A focused campaign targeting these 500 people with personalized offers, early access to new products, or VIP treatment would be highly cost-effective.
Business Implications and Strategic Recommendations
These predictions enable several strategic decisions that would be impossible without the models:
Marketing budget allocation: Instead of spreading your budget evenly across 18,000 customers, concentrate resources on the 1,953 customers in High and Very High tiers (11% of the base). These customers generate 56% of predicted revenue. Even expensive interventions like personal calls or custom offers become economically viable.
Reactivation prioritization: Among inactive customers, target only those with high historical value and relatively recent lapse. The model identifies which inactive customers are worth reactivation efforts and which should be written off. This prevents wasting money on lost causes.
Inventory planning: The predicted revenue of $347,000 provides a baseline for inventory decisions. If your margin is 40%, you need roughly $208,000 in cost of goods sold to support this revenue. This informs purchasing decisions and working capital planning.
Performance monitoring: When actual 2016 results arrive, compare them to predictions. Large deviations (positive or negative) signal changes in customer behavior requiring investigation. Did a competitor enter the market? Did product quality improve or decline? Did economic conditions shift? The predictions become a benchmark for detecting changes.
Segment-specific campaigns: Different value tiers need different messaging. Very High customers might receive “Thank you for being a VIP” messages with exclusive benefits. High customers get “You’re important to us” communications with loyalty rewards. Medium customers receive standard promotional offers. This segmentation makes marketing more efficient and relevant.
Churn risk identification: Customers with historically high spending but currently low predicted probability are at risk. Their past value makes them worth saving. Proactive outreach asking “What can we do better?” might prevent churn before it’s permanent.
Model Maintenance and Deployment Considerations
Deploying these models in production requires thinking beyond the initial analysis. Several practical issues emerge:
Retraining cadence: Customer behavior changes over time. Models trained on 2014-2015 data will gradually lose accuracy as we move further into 2016 and beyond. Most businesses retrain quarterly or annually, depending on how fast their market evolves. Fast-moving consumer goods might need monthly updates. Durable goods might be fine with annual retraining.
Feature engineering evolution: Our simple RFM features work well, but you might discover additional predictors. Seasonality patterns, product category preferences, channel behavior (web vs. mobile), and demographic information could all improve predictions. The key is balancing complexity against maintenance burden.
Threshold calibration: The score thresholds we used ($10, $30, $50) work for this dataset, but your business might need different cutoffs. If your profit margins are high, you can afford to target more customers. If margins are thin, focus more narrowly on the very top tier. The thresholds should reflect your unit economics.
Integration architecture: Predictions need to flow into your CRM, email marketing platform, and advertising systems. This typically requires building data pipelines that automatically generate updated scores and push them to downstream systems. Manual uploads don’t scale and introduce error risk.
Feedback loops: Track which predicted-high-value customers actually convert and which don’t. This data helps refine models over time. If certain customer profiles consistently underperform predictions, adjust your features or segmentation. Machine learning systems improve through iteration, not one-time deployment.
Explainability and trust: Stakeholders need to understand why a customer received a high score. “The black box said so” doesn’t build confidence. Being able to explain “This customer scores high because they purchased frequently, recently, and at high dollar values” builds trust in the system. Our simple linear models have this advantage over complex neural networks.
Looking Ahead: From Predictions to Lifetime Value
We’ve made substantial progress in our customer analytics journey. The first tutorial taught us to discover natural customer groupings through hierarchical clustering. The second showed us how to translate business logic directly into actionable segments. Today we learned to predict next-period behavior using statistical models.
But we’re not done yet. These predictions answer “what will customers do next year?” The ultimate question remains unanswered: “what is each customer worth over their entire relationship with our company?”
That’s where Customer Lifetime Value (CLV) comes in. CLV extends our one-year predictions to multi-year horizons. Instead of asking “will this customer buy next quarter?” we ask “how much total value will this customer generate over the next five or ten years?” This shift from short-term prediction to long-term valuation transforms how we think about customer relationships.
Our next tutorial completes the series by building a CLV model using Markov chains. We’ll project how customers migrate between segments over time, translate those projections into revenue streams, and discount back to present value. The result will be a single number that tells you what each customer is truly worth.
Understanding CLV changes everything. It tells you how much you can afford to spend acquiring customers. It guides retention investments by quantifying the cost of losing different customer types. It prioritizes product development by showing which customer segments create the most value. CLV is the capstone metric that unifies all our previous work.
Conclusion
Predicting customer behavior is challenging but achievable. Our two-model approach (probability of purchase and amount spent) provides a practical framework that balances statistical rigor with business usability. The retrospective validation using 2014-2015 data builds confidence before making real-money decisions on 2016 predictions.
The models we built are deliberately simple. Five RFM features, logistic regression, and ordinary least squares. No deep learning, no ensemble methods, no exotic algorithms. This simplicity is a feature, not a bug. Simple models are easier to understand, maintain, debug, and explain. They train quickly and integrate easily into existing systems. For most businesses, simple models deliver 80% of the value with 20% of the complexity.
The business value comes not from algorithmic sophistication but from systematic application. A simple model used consistently beats a sophisticated model gathering dust. The organizations that win at customer analytics aren’t necessarily those with the fanciest algorithms. They’re the ones who integrate insights into decision processes, measure results, and iterate based on what they learn.
Our predicted customer scores provide a foundation for smarter marketing investment. Focus resources on high-probability, high-value customers. Develop segment-specific campaigns matched to customer potential. Monitor performance against predictions to detect changes quickly. Use the models as decision support tools, not autopilot systems.
These predictions set the stage for the final piece of our framework: Customer Lifetime Value. In our next and final tutorial, we’ll extend these single-period predictions to multi-year projections, giving you the complete picture of customer value from first purchase to final transaction. That’s where this journey leads.
References
-
Lilien, Gary L, Arvind Rangaswamy, and Arnaud De Bruyn. 2017. Principles of Marketing Engineering and Analytics. State College, PA: DecisionPro.
-
Arnaud De Bruyn. Foundations of Marketing Analytics (MOOC). Coursera.
-
Hosmer, David W., Stanley Lemeshow, and Rodney X. Sturdivant. 2013. Applied Logistic Regression. 3rd ed. Hoboken, NJ: Wiley.
-
James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2021. An Introduction to Statistical Learning: With Applications in R. 2nd ed. New York: Springer.
-
Fader, Peter S., and Bruce G. S. Hardie. 2009. “Probability Models for Customer-Base Analysis.” Journal of Interactive Marketing 23 (1): 61-69.
-
Dataset from Github repo. Accessed 15 December 2021.
Business Analytics Tutorial 