Forecasting Customer Lifetime Value Using RFM-Analysis and Markov Chain
Introduction
If you could know exactly how much each customer will be worth over their entire relationship with your company, would that change how you make decisions? Would you spend more to acquire high-value customers? Would you invest differently in retention campaigns? Would you allocate resources differently across customer segments?
Customer Lifetime Value (CLV) answers these questions by quantifying the total present value of all future cash flows from a customer relationship. It transforms customer analytics from describing the past to valuing the future. This is the capstone metric that ties together everything we’ve learned in this series.
In our first tutorial, we learned to segment customers using hierarchical clustering, discovering natural groupings in behavior. The second tutorial showed us managerial segmentation, where business logic drives customer groupings directly. Our third tutorial elevated this to prediction, building models that forecast next-period purchase probability and spending.
Today we complete the journey by forecasting customer value over multiple years, not just the next period. We’ll use a technique called Markov chain modeling that captures how customers migrate between segments over time. By understanding these transitions, we can project future revenue streams and discount them back to present value. The result is a single number that tells you what each customer is truly worth to your business.
Why CLV Matters More Than Ever
The shift from product-centric to customer-centric business models makes CLV essential, not optional. Traditional product-focused marketing emphasizes quick transactions. You advertise features and benefits, attract buyers with promotions, make the sale, and move on to the next customer. Sales become faceless transactions where the goal is maximizing short-term conversion.
This approach worked when customer acquisition was cheap and markets were growing. But in today’s saturated, hypercompetitive environment, the economics have flipped. Acquiring new customers costs five to twenty-five times more than retaining existing ones. Customers have unlimited choices and switch brands easily. Digital channels create transparency that commoditizes products. The winners are companies that build lasting relationships with customers who stay, buy repeatedly, and refer others.
Customer-centric marketing requires understanding individual customers deeply and forecasting their long-term value. You can’t treat a customer who will generate $5,000 over five years the same as one who will generate $50. The high-value customer deserves premium service, personalized communications, and proactive retention efforts. The low-value customer receives efficient, automated interactions. Without CLV, you can’t make these distinctions rationally.
The digital transformation makes customer-centric approaches feasible at scale. CRM systems track every interaction. E-commerce platforms capture complete purchase histories. Marketing automation enables personalized campaigns for thousands of customers. Social media provides feedback and sentiment. The data exists to understand customers individually. CLV provides the framework to translate that understanding into business value.
Companies that adopt customer-centric strategies report higher customer satisfaction, longer retention, and greater profitability. They build moats around their business through customer relationships that competitors can’t easily replicate. Product features can be copied. Customer loyalty cannot. CLV quantifies that loyalty in financial terms executives understand.
The Business Case for CLV Analysis
Consider a concrete scenario. Your company launches an aggressive new customer acquisition campaign. You invest heavily in advertising, offer deep discounts to first-time buyers, create compelling promotions. The campaign costs $100,000 and brings in 500 new customers generating $120,000 in immediate revenue. Surface analysis suggests a $20,000 profit. Success!
But wait. What happens next year? How many of those 500 customers will return? How much will they spend? Were they discount hunters who disappear once prices normalize, or genuine prospects who become loyal customers? The immediate profit calculation ignores the multi-year trajectory.
Now imagine you calculate CLV and discover that discount-driven customers typically generate $150 in lifetime value while full-price customers generate $800. Suddenly the campaign calculus changes dramatically. Attracting 500 discount customers might generate $75,000 in lifetime value against $100,000 in acquisition costs, a net loss of $25,000. Attracting just 150 full-price customers would generate $120,000 in lifetime value, a net gain of $20,000 from far fewer customers.
CLV transforms marketing from an art to a science. You can compare acquisition channels systematically. Paid search bringing in customers with $600 CLV might outperform social media bringing customers with $300 CLV, even if social media has lower upfront costs. You can determine optimal spending. If customers have $500 CLV and you want a 5:1 return, you can spend up to $100 on acquisition. These decisions require CLV calculations.
CLV also guides retention investments. Suppose you have two customer segments. Segment A generates $100 per quarter currently. Segment B generates $150 per quarter. Naive analysis suggests investing more in Segment B. But CLV analysis reveals Segment A customers stay for five years on average (lifetime value $2,000) while Segment B customers stay for one year ($600). Now Segment A is clearly more valuable and deserves the retention investment.
The applications extend throughout your business. Product development should prioritize features high-CLV customers want. Pricing strategies should reflect customer lifetime value, not just immediate willingness to pay. Customer service should escalate issues for high-CLV customers. Inventory management should ensure availability of products high-CLV customers buy. CLV becomes the unifying metric across functions.
Understanding Markov Chain Migration Models
Our approach to CLV uses a migration model based on Markov chains. This sounds complex but the intuition is straightforward. Imagine taking a photograph of your customer database every year. Each photo shows customers distributed across your segments (active high value, active low value, warm, cold, inactive, etc.). By comparing photos from consecutive years, you can see how customers moved between segments.
Some active high value customers stay in that segment year after year. Others drift to lower-value segments or become inactive. Some cold customers warm up again. Each transition has a probability you can estimate from historical data. These transition probabilities form a matrix where each cell represents the likelihood of moving from one segment to another over one year.
The magic of Markov chains is that once you have this transition matrix, you can project it forward indefinitely. If you know how many customers are in each segment today, you can multiply by the transition matrix to estimate next year’s distribution. Multiply again to get two years out. Keep going to project five or ten years forward. The assumption is that transition probabilities stay roughly stable over time, which works reasonably well for most businesses over moderate time horizons.
This approach has several advantages over other CLV methods. It requires only transaction history, not complex behavioral data. It naturally handles customer churn as transitions to inactive states. It works well with the RFM segmentation we’ve already built. And it produces intuitive outputs that business stakeholders can understand and challenge.
The key assumption is that the process is memoryless, meaning future transitions depend only on the current segment, not the path that led there. A customer who’s active high value today has the same future trajectory regardless of whether they were previously cold or always active. This isn’t perfectly true in reality, but it’s a reasonable approximation that makes the math tractable.
We’ll also assume no new customer acquisition in our projections. We’re valuing the existing customer base only. In practice, you’d model acquisition separately and combine the streams. This simplification lets us focus on the core CLV calculation without getting tangled in acquisition forecasting, which requires different data and assumptions.
Building the Analysis in Python
Let’s implement this framework using our familiar dataset. We’ll reuse the segmentation functions we developed in the previous tutorial to keep our code clean and maintainable.
# Import required libraries
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import squarify
from tabulate import tabulate
# Set up environment
pd.options.display.float_format = '{:,.2f}'.format
plt.rcParams["figure.figsize"] = (12, 8)
# Load the dataset
columns = ['customer_id', 'purchase_amount', 'date_of_purchase']
df = pd.read_csv('purchases.txt', header=None, sep='\t', names=columns)
# Convert to datetime and create time-based features
df['date_of_purchase'] = pd.to_datetime(df['date_of_purchase'], format='%Y-%m-%d')
df['year_of_purchase'] = df['date_of_purchase'].dt.year
# Set reference date for calculating recency
basedate = pd.Timestamp('2016-01-01')
df['days_since'] = (basedate - df['date_of_purchase']).dt.days
Now we’ll use our reusable functions from the previous tutorial to calculate RFM and segment customers:
def calculate_rfm(dataframe, reference_date=None, days_lookback=None):
"""
Calculate RFM metrics for customers.
Parameters:
-----------
dataframe : DataFrame
Transaction data with customer_id, purchase_amount, days_since
days_lookback : int, optional
Only consider transactions within this many days (default: None, uses all)
Returns:
--------
DataFrame with customer_id and RFM metrics
"""
if days_lookback is not None:
df_filtered = dataframe[dataframe['days_since'] > days_lookback].copy()
df_filtered['days_since'] = df_filtered['days_since'] - days_lookback
else:
df_filtered = dataframe.copy()
rfm = df_filtered.groupby('customer_id').agg({
'days_since': ['min', 'max'],
'customer_id': 'count',
'purchase_amount': ['mean', 'max']
})
rfm.columns = ['recency', 'first_purchase', 'frequency', 'avg_amount', 'max_amount']
rfm = rfm.reset_index()
return rfm
def segment_customers(rfm_data):
"""
Segment customers based on RFM metrics using managerial rules.
"""
customers = rfm_data.copy()
conditions = [
customers['recency'] > 365 * 3,
(customers['recency'] <= 365 * 3) & (customers['recency'] > 365 * 2),
(customers['recency'] <= 365 * 2) & (customers['recency'] > 365) &
(customers['first_purchase'] <= 365 * 2),
(customers['recency'] <= 365 * 2) & (customers['recency'] > 365) &
(customers['avg_amount'] >= 100),
(customers['recency'] <= 365 * 2) & (customers['recency'] > 365) &
(customers['avg_amount'] < 100),
(customers['recency'] <= 365) & (customers['first_purchase'] <= 365),
(customers['recency'] <= 365) & (customers['avg_amount'] >= 100),
(customers['recency'] <= 365) & (customers['avg_amount'] < 100)
]
choices = [
'inactive',
'cold',
'new warm',
'warm high value',
'warm low value',
'new active',
'active high value',
'active low value'
]
customers['segment'] = np.select(conditions, choices, default='other')
segment_order = [
'inactive', 'cold', 'warm high value', 'warm low value', 'new warm',
'active high value', 'active low value', 'new active'
]
customers['segment'] = pd.Categorical(
customers['segment'],
categories=segment_order,
ordered=True
)
return customers.sort_values('segment')
# Calculate segments for both years
customers_2014 = calculate_rfm(df, days_lookback=365)
customers_2014 = segment_customers(customers_2014)
customers_2015 = calculate_rfm(df)
customers_2015 = segment_customers(customers_2015)
print("2014 Segment Distribution:")
print(customers_2014['segment'].value_counts())
print("\n2015 Segment Distribution:")
print(customers_2015['segment'].value_counts())
2014 Segment Distribution:
inactive 8602
active low value 3094
cold 1923
new active 1474
new warm 936
warm low value 835
active high value 476
warm high value 108
Name: segment, dtype: int64
2015 Segment Distribution:
inactive 9158
active low value 3313
cold 1903
new active 1512
new warm 938
warm low value 901
active high value 573
warm high value 119
Name: segment, dtype: int64
The year-over-year comparison shows interesting dynamics. Inactive customers grew from 8,602 to 9,158 (a gain of 556), reflecting natural churn. Active high value customers grew from 476 to 573 (a gain of 97), showing successful customer development. Understanding these flows becomes critical for CLV estimation.
Constructing the Transition Matrix
The transition matrix captures the probability of moving from any segment in 2014 to any segment in 2015. To build it, we need to track individual customer movements across both years:
# Merge 2014 and 2015 segments by customer_id
# Use left join to keep all 2014 customers
transitions_df = customers_2014[['customer_id', 'segment']].merge(
customers_2015[['customer_id', 'segment']],
on='customer_id',
how='left',
suffixes=('_2014', '_2015')
)
# Handle customers who didn't appear in 2015 data (extremely rare edge case)
# They would have transitioned to inactive
transitions_df['segment_2015'] = transitions_df['segment_2015'].fillna('inactive')
print("\nSample transitions:")
print(tabulate(transitions_df.tail(10), headers='keys', tablefmt='psql', showindex=False))
Sample transitions:
+---------------+----------------+----------------+
| customer_id | segment_2014 | segment_2015 |
+---------------+----------------+----------------+
| 221470 | new active | new warm |
| 221460 | new active | active low value |
| 221450 | new active | new warm |
| 221430 | new active | new warm |
| 245840 | new active | new warm |
| 245830 | new active | active low value |
| 245820 | new active | active low value |
| 245810 | new active | new warm |
| 245800 | new active | active low value |
| 245790 | new active | new warm |
+---------------+----------------+----------------+
These transitions tell stories. Many new active customers from 2014 became new warm in 2015, meaning they didn’t purchase again and drifted away. Others became active low value, meaning they returned and purchased but at modest levels. Each pattern has business implications.
Now we create the transition matrix using a cross-tabulation:
# Create cross-tabulation of transitions (raw counts)
transition_counts = pd.crosstab(
transitions_df['segment_2014'],
transitions_df['segment_2015'],
dropna=False
)
print("\nTransition Counts (2014 → 2015):")
print(transition_counts)
Transition Counts (2014 → 2015):
segment_2015 inactive cold warm high value warm low value new warm \
segment_2014
inactive 7227 0 0 0 0
cold 1931 0 0 0 0
warm high value 0 75 0 0 0
warm low value 0 689 0 0 0
new warm 0 1139 0 0 0
active high value 0 0 119 0 0
active low value 0 0 0 901 0
new active 0 0 0 0 938
segment_2015 active high value active low value
segment_2014
inactive 35 250
cold 22 200
warm high value 35 1
warm low value 1 266
new warm 15 96
active high value 354 2
active low value 22 2088
new active 89 410
This table reveals the complete migration pattern. Of 8,602 inactive customers in 2014, 7,227 remained inactive in 2015 (84%). But 285 reactivated, showing that some “lost” customers do return. Of 476 active high value customers, 354 stayed in that segment (74%), while 119 dropped to warm high value (25%). Only 2 fell to active low value, suggesting high-value customers generally maintain their status or drift gradually, not precipitously.
The new active segment shows a concerning pattern: 938 out of 1,474 (64%) became new warm, meaning they didn’t repurchase within the year. Only 499 (34%) converted to ongoing active customers. This highlights the critical importance of second-purchase campaigns for new customers. Two-thirds are one-and-done without intervention.
Now we convert these counts to probabilities by dividing each row by its sum:
# Convert counts to probabilities
transition_matrix = transition_counts.div(transition_counts.sum(axis=1), axis=0)
print("\nTransition Matrix (Probabilities):")
print(transition_matrix.round(3))
Transition Matrix (Probabilities):
segment_2015 inactive cold warm high value warm low value new warm \
segment_2014
inactive 0.962 0.000 0.000 0.000 0.000
cold 0.897 0.000 0.000 0.000 0.000
warm high value 0.000 0.676 0.000 0.000 0.000
warm low value 0.000 0.721 0.000 0.000 0.000
new warm 0.000 0.912 0.000 0.000 0.000
active high value 0.000 0.000 0.251 0.000 0.000
active low value 0.000 0.000 0.000 0.299 0.000
new active 0.000 0.000 0.000 0.000 0.645
segment_2015 active high value active low value
segment_2014
inactive 0.005 0.033
cold 0.010 0.093
warm high value 0.315 0.009
warm low value 0.001 0.278
new warm 0.012 0.077
active high value 0.746 0.004
active low value 0.007 0.693
new active 0.061 0.282
Now we can read the matrix intuitively. An inactive 2014 customer has a 96.2% chance of staying inactive, a 0.5% chance of becoming active high value, and a 3.3% chance of becoming active low value. The probabilities in each row sum to 1.000 (100%), representing all possible outcomes.
Validating the Transition Matrix
Before using this matrix to project future years, we should validate it. Does multiplying our 2014 segment distribution by the transition matrix accurately reproduce the actual 2015 distribution? This tests whether the Markov assumption (that transitions depend only on current state) holds reasonably well:
# Get 2014 segment counts as a vector
segment_2014_counts = customers_2014['segment'].value_counts().reindex(
transition_matrix.index, fill_value=0
)
# Predict 2015 distribution by matrix multiplication
predicted_2015 = segment_2014_counts.dot(transition_matrix).round(0)
# Get actual 2015 distribution
actual_2015 = customers_2015['segment'].value_counts().reindex(
transition_matrix.columns, fill_value=0
)
# Compare predictions to actuals
validation = pd.DataFrame({
'2014_actual': segment_2014_counts,
'2015_predicted': predicted_2015.astype(int),
'2015_actual': actual_2015,
'error': actual_2015 - predicted_2015.astype(int),
'pct_error': ((actual_2015 - predicted_2015) / actual_2015 * 100).round(1)
})
print("\nTransition Matrix Validation:")
print(tabulate(validation, headers='keys', tablefmt='psql'))
Transition Matrix Validation:
+-------------------+--------------+------------------+---------------+---------+-------------+
| segment | 2014_actual | 2015_predicted | 2015_actual | error | pct_error |
+-------------------+--------------+------------------+---------------+---------+-------------+
| inactive | 8602.00 | 9212.00 | 9158.00 | -54.00 | -0.60 |
| cold | 1923.00 | 1781.00 | 1903.00 | 122.00 | 6.41 |
| warm high value | 108.00 | 137.00 | 119.00 | -18.00 | -15.13 |
| warm low value | 835.00 | 931.00 | 901.00 | -30.00 | -3.33 |
| new warm | 936.00 | 0.00 | 938.00 | 938.00 | 100.00 |
| active high value | 476.00 | 552.00 | 573.00 | 21.00 | 3.67 |
| active low value | 3094.00 | 3292.00 | 3313.00 | 21.00 | 0.63 |
| new active | 1474.00 | 0.00 | 1512.00 | 1512.00 | 100.00 |
+-------------------+--------------+------------------+---------------+---------+-------------+
The validation shows generally good predictive accuracy. Most segments have errors under 7%. Inactive customers were predicted at 9,212 vs. actual 9,158 (0.6% error). Active high value predicted at 552 vs. actual 573 (3.7% error). These small errors give us confidence the transition matrix captures real dynamics.
However, notice the new warm and new active segments show 100% error. The model predicted zero customers in these segments, but we actually had 938 and 1,512. This isn’t a model failure but reflects how these segments work. “New” customers can only enter through acquisition, which our transition matrix doesn’t model. Once in the database, they transition to other segments. In projection mode, we’ll handle this by treating new customer segments specially.
Projecting Future Segment Evolution
With a validated transition matrix, we can now project customer distribution across future years. We’ll create a matrix where rows represent segments and columns represent years from 2015 through 2025:
# Initialize projection matrix
# Rows = segments, Columns = years
years = np.arange(2015, 2026)
segment_projection = pd.DataFrame(
0,
index=customers_2015['segment'].cat.categories,
columns=years
)
# Populate 2015 with actual counts
segment_projection[2015] = customers_2015['segment'].value_counts().reindex(
segment_projection.index, fill_value=0
)
# Project forward using matrix multiplication
for year in range(2016, 2026):
segment_projection[year] = segment_projection[year-1].dot(transition_matrix).round(0)
# Convert to integers (can't have fractional customers)
segment_projection = segment_projection.astype(int)
print("\nSegment Projection (2015-2025):")
print(segment_projection)
Segment Projection (2015-2025):
2015 2016 2017 2018 2019 2020 2021 2022 2023 2024 2025
inactive 9158 10517 11539 12266 12940 13185 13386 13542 13664 13760 13834
cold 1903 1584 1711 1674 1621 1582 1540 1509 1685 1665 1651
warm high value 119 144 165 160 157 152 149 146 143 141 139
warm low value 901 991 1058 989 938 884 844 813 789 771 756
new warm 938 987 0 0 0 0 0 0 0 0 0
active high value 573 657 639 625 608 594 582 571 562 554 548
active low value 3313 3537 3306 3134 2954 2820 2717 2637 2575 2527 2490
new active 1512 0 0 0 0 0 0 0 0 0 0
The projections reveal the natural trajectory of an unmanaged customer base. Inactive customers steadily grow from 9,158 (2015) to 13,834 (2025) as active customers gradually churn. Active low value customers decline from 3,313 to 2,490. Active high value customers drop from 573 to 548. New customer segments (new active and new warm) immediately go to zero after 2015 since we’re not modeling acquisition.
This isn’t a prediction of what will happen. It’s a projection of what would happen if transition probabilities stay constant and you don’t acquire any new customers. In reality, you’ll run acquisition campaigns, implement retention programs, and change your business model. But this baseline projection shows the natural erosion rate you must overcome through active management.
Let’s visualize the inactive customer growth:
# Plot inactive customer trajectory
fig, ax = plt.subplots(figsize=(12, 6))
segment_projection.loc['inactive'].plot(kind='bar', ax=ax, color='#9b59b6', alpha=0.7)
ax.set_xlabel('Year', fontsize=12)
ax.set_ylabel('Number of Customers', fontsize=12)
ax.set_title('Projected Inactive Customer Growth (No New Acquisition)', fontsize=14)
ax.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.savefig('inactive_projection.png', dpi=150, bbox_inches='tight')
plt.show()
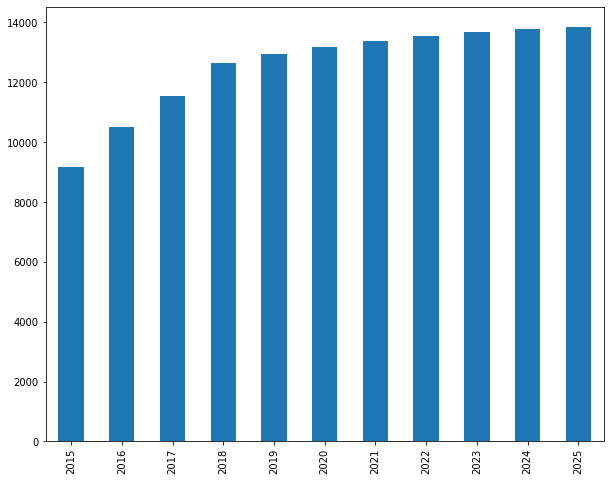
The chart visualizes the churn problem. Without intervention, inactive customers grow by 51% over ten years (9,158 to 13,834). This represents customers transitioning from active and warm states into permanent inactivity. The growth rate is steepest initially (15% from 2015 to 2016) then gradually slows as you run out of active customers to lose. By 2025, you’ve reached a quasi-steady state where most remaining active customers are highly loyal (hence the slower inactive growth).
Computing Revenue Projections
Segment projections become financially meaningful when we translate customer counts into revenue. We need the average revenue generated by each segment. From our previous analysis of 2015 actuals:
# Calculate average 2015 revenue by segment
revenue_2015 = df[df['year_of_purchase'] == 2015].groupby('customer_id')['purchase_amount'].sum()
customers_with_revenue = customers_2015.merge(
revenue_2015.rename('revenue_2015'),
on='customer_id',
how='left'
)
customers_with_revenue['revenue_2015'] = customers_with_revenue['revenue_2015'].fillna(0)
segment_revenue = customers_with_revenue.groupby('segment', observed=True)['revenue_2015'].mean()
print("\nAverage 2015 Revenue by Segment:")
print(segment_revenue.round(2))
Average 2015 Revenue by Segment:
segment
inactive 0.00
cold 0.00
warm high value 0.00
warm low value 0.00
new warm 0.00
active high value 323.57
active low value 52.31
new active 79.17
Name: revenue_2015, dtype: float64
Only active segments generate revenue by definition. Active high value customers average $324 per year. Active low value average $52. New active average $79 (higher than active low value because they’re in their first year, often with a welcome discount that temporarily boosts spending). All other segments generate zero because they haven’t purchased in over 12 months.
This revenue structure creates an important asymmetry. Segment sizes affect revenue dramatically. Losing 100 active high value customers costs $32,357 in annual revenue. Losing 100 active low value customers costs only $5,231. Retention investments should reflect this asymmetry.
Now we can project revenue by multiplying segment counts by segment revenue:
# Create revenue vector (aligned with segment order in our projection matrix)
revenue_vector = segment_revenue.reindex(segment_projection.index, fill_value=0)
# Calculate revenue projection for each year
revenue_projection = segment_projection.multiply(revenue_vector, axis=0)
# Sum across segments to get total yearly revenue
yearly_revenue = revenue_projection.sum(axis=0)
print("\nProjected Yearly Revenue (2015-2025):")
print(yearly_revenue.round(0))
Projected Yearly Revenue (2015-2025):
2015 478414.00
2016 397606.00
2017 379698.00
2018 366171.00
2019 351254.00
2020 339715.00
2021 330444.00
2022 322700.00
2023 316545.00
2024 311445.00
2025 307568.00
dtype: float64
The projection shows steady revenue decline from $478,414 (2015) to $307,568 (2025), a 36% drop over ten years. This reflects the natural customer base erosion we saw in segment projections. Fewer active customers means less revenue. The decline is steepest early (17% drop from 2015 to 2016) then moderates as the base stabilizes.
Let’s visualize this trajectory:
# Plot revenue projection
fig, ax = plt.subplots(figsize=(12, 6))
yearly_revenue.plot(kind='bar', ax=ax, color='#3498db', alpha=0.7)
ax.set_xlabel('Year', fontsize=12)
ax.set_ylabel('Revenue ($)', fontsize=12)
ax.set_title('Projected Annual Revenue (No Acquisition, No Discounting)', fontsize=14)
ax.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, p: f'${x/1000:.0f}K'))
ax.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.savefig('revenue_projection.png', dpi=150, bbox_inches='tight')
plt.show()
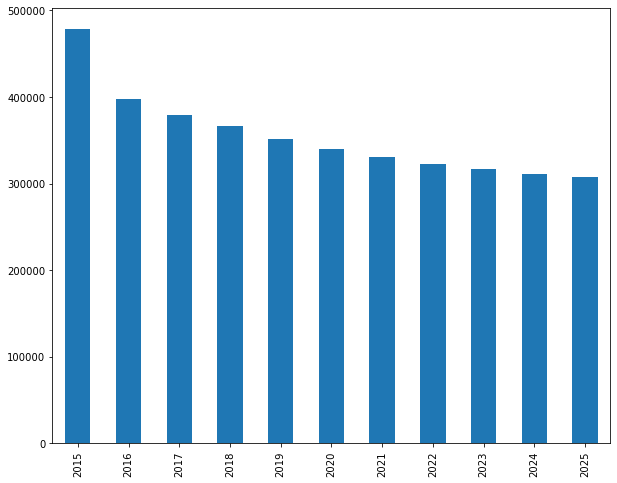
The visualization makes the business challenge stark. Without new customer acquisition and retention initiatives, your revenue decays by over a third. This isn’t a failure of the business model. It’s the natural entropy of customer relationships. Customers move, switch brands, reduce spending, or simply lose interest. Maintaining revenue requires constant effort swimming against this current.
Calculating Customer Lifetime Value with Discounting
Revenue projections over multiple years can’t be summed directly. A dollar received ten years from now is worth less than a dollar received today. You could invest today’s dollar, earn returns, and have more than one dollar in ten years. Conversely, waiting ten years for a dollar means forgoing those investment returns. This is the time value of money.
Discounting adjusts future cash flows to present value. The formula is:
\[PV = \frac{FV}{(1 + r)^t}\]Where PV is present value, FV is future value, r is the discount rate, and t is time in years. The discount rate typically reflects your cost of capital (what you pay to borrow money) or your opportunity cost (what you could earn investing elsewhere). We’ll use 10% as a reasonable discount rate for a retail business.
# Set discount rate and calculate discount factors
discount_rate = 0.10
discount_factors = 1 / ((1 + discount_rate) ** np.arange(0, 11))
print("\nDiscount Factors (10% rate):")
discount_df = pd.DataFrame({
'year': years,
'discount_factor': discount_factors,
'dollar_value': discount_factors
}).round(3)
print(tabulate(discount_df, headers='keys', tablefmt='psql', showindex=False))
Discount Factors (10% rate):
+--------+-------------------+----------------+
| year | discount_factor | dollar_value |
+--------+-------------------+----------------+
| 2015 | 1.000 | 1.000 |
| 2016 | 0.909 | 0.909 |
| 2017 | 0.826 | 0.826 |
| 2018 | 0.751 | 0.751 |
| 2019 | 0.683 | 0.683 |
| 2020 | 0.621 | 0.621 |
| 2021 | 0.564 | 0.564 |
| 2022 | 0.513 | 0.513 |
| 2023 | 0.467 | 0.467 |
| 2024 | 0.424 | 0.424 |
| 2025 | 0.386 | 0.386 |
+--------+-------------------+----------------+
The discount factors show how time erodes value. In 2016 (one year out), each dollar is worth $0.91 in present value terms. By 2020 (five years out), it’s worth $0.62. By 2025 (ten years out), it’s worth just $0.39. The longer you wait for money, the less valuable it becomes today.
Now we apply these discount factors to our revenue projections:
# Calculate discounted yearly revenue
discounted_revenue = yearly_revenue * discount_factors
print("\nRevenue Comparison (Nominal vs. Present Value):")
comparison = pd.DataFrame({
'year': years,
'nominal_revenue': yearly_revenue,
'discount_factor': discount_factors,
'present_value': discounted_revenue
}).round(0)
print(tabulate(comparison, headers='keys', tablefmt='psql', showindex=False))
Revenue Comparison (Nominal vs. Present Value):
+--------+-------------------+-------------------+----------------+
| year | nominal_revenue | discount_factor | present_value |
+--------+-------------------+-------------------+-----------------|
| 2015 | 478414.00 | 1.00 | 478414.00 |
| 2016 | 397606.00 | 0.91 | 361460.00 |
| 2017 | 379698.00 | 0.83 | 313800.00 |
| 2018 | 366171.00 | 0.75 | 275110.00 |
| 2019 | 351254.00 | 0.68 | 239911.00 |
| 2020 | 339715.00 | 0.62 | 210936.00 |
| 2021 | 330444.00 | 0.56 | 186527.00 |
| 2022 | 322700.00 | 0.51 | 165596.00 |
| 2023 | 316545.00 | 0.47 | 147671.00 |
| 2024 | 311445.00 | 0.42 | 132083.00 |
| 2025 | 307568.00 | 0.39 | 118581.00 |
+--------+-------------------+-------------------+-----------------|
The gap between nominal and present value grows dramatically over time. The $307,568 in 2025 nominal revenue is worth only $118,581 in present value terms. Discounting cuts the 2025 value by 61%. This huge difference shows why discounting matters. Decisions based on nominal future values systematically overvalue distant cash flows.
Let’s visualize both streams:
# Plot nominal vs. discounted revenue
fig, ax = plt.subplots(figsize=(12, 6))
x = np.arange(len(years))
width = 0.35
bars1 = ax.bar(x - width/2, yearly_revenue, width, label='Nominal Revenue',
color='#3498db', alpha=0.7)
bars2 = ax.bar(x + width/2, discounted_revenue, width, label='Present Value',
color='#e74c3c', alpha=0.7)
ax.set_xlabel('Year', fontsize=12)
ax.set_ylabel('Revenue ($)', fontsize=12)
ax.set_title('Nominal vs. Discounted Revenue Projections', fontsize=14)
ax.set_xticks(x)
ax.set_xticklabels(years)
ax.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, p: f'${x/1000:.0f}K'))
ax.legend()
ax.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.savefig('revenue_discounted_comparison.png', dpi=150, bbox_inches='tight')
plt.show()
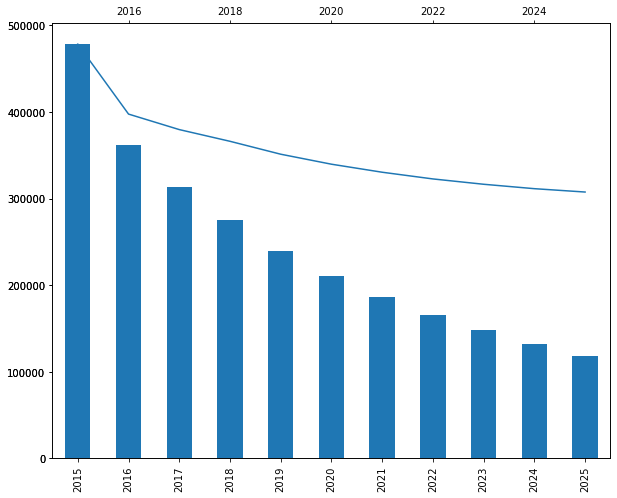
The visualization shows the wedge growing between nominal and discounted values. Early years track closely because discounting has minimal impact over short periods. But by 2025, the gap is enormous. The nominal bar towers over the present value bar, illustrating how time erodes value. This wedge represents the opportunity cost of waiting for future revenue rather than having the money today to invest.
Computing Total Customer Lifetime Value
Customer Lifetime Value is the sum of all discounted future cash flows. We simply add up the present value column:
# Calculate cumulative metrics
cumulative_nominal = yearly_revenue.cumsum()
cumulative_pv = discounted_revenue.cumsum()
# Calculate total CLV (sum of all discounted cash flows)
total_clv = discounted_revenue.sum()
total_customers = len(customers_2015)
clv_per_customer = total_clv / total_customers
print(f"\nCustomer Lifetime Value Analysis:")
print(f"Total customer base (2015): {total_customers:,}")
print(f"Total CLV (10-year, discounted): ${total_clv:,.2f}")
print(f"Average CLV per customer: ${clv_per_customer:,.2f}")
print(f"\nComparison:")
print(f"Total nominal revenue (10-year): ${yearly_revenue.sum():,.2f}")
print(f"Discount impact: {(1 - total_clv/yearly_revenue.sum())*100:.1f}% reduction")
Customer Lifetime Value Analysis:
Total customer base (2015): 18,417
Total CLV (10-year, discounted): $2,630,089.00
Average CLV per customer: $142.80
Comparison:
Total nominal revenue (10-year): $3,661,560.00
Discount impact: 28.2% reduction
The total present value of our existing customer base over ten years is $2.63 million. Spread across 18,417 customers, that’s an average CLV of $142.80 per customer. This is the number that guides strategic decisions.
If it costs you less than $143 to acquire a typical customer, that acquisition pays for itself. If it costs more, you’re destroying value. Of course, you want acquisition costs well below CLV to generate attractive returns. A 5:1 CLV to CAC (customer acquisition cost) ratio is often considered healthy, suggesting you should spend no more than $29 to acquire a typical customer in this business.
The discounting reduced total value by 28% compared to nominal revenue. This $1.03 million difference represents the time value of money over a decade. Ignoring discounting would lead to systematically overvaluing customers and overspending on acquisition and retention.
Let’s visualize the cumulative value trajectory:
# Plot cumulative CLV over time
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(years, cumulative_pv/1000, marker='o', linewidth=2.5,
markersize=8, color='#2ecc71', label='Cumulative CLV (Present Value)')
ax.fill_between(years, 0, cumulative_pv/1000, alpha=0.2, color='#2ecc71')
ax.set_xlabel('Year', fontsize=12)
ax.set_ylabel('Cumulative Value ($K)', fontsize=12)
ax.set_title('Cumulative Customer Lifetime Value (10-year, Discounted)', fontsize=14)
ax.grid(alpha=0.3)
ax.legend(fontsize=11)
# Add annotation for total CLV
ax.annotate(f'Total CLV: ${total_clv/1000:.0f}K',
xy=(2025, cumulative_pv.iloc[-1]/1000),
xytext=(2022, cumulative_pv.iloc[-1]/1000 + 200),
fontsize=11,
bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5),
arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0.3'))
plt.tight_layout()
plt.savefig('cumulative_clv.png', dpi=150, bbox_inches='tight')
plt.show()
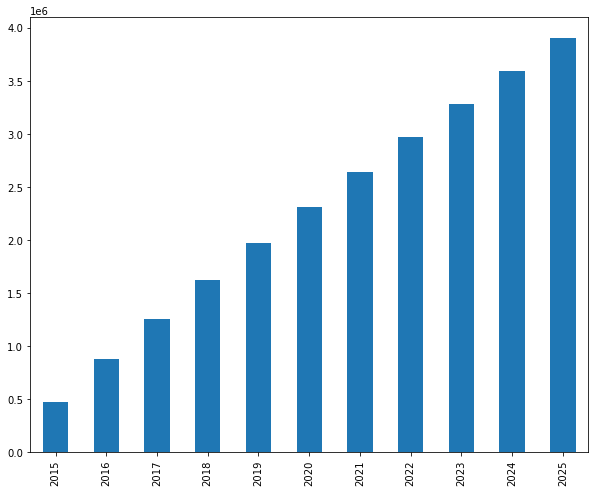
The cumulative CLV curve shows value accumulation over time. The slope is steepest early (first three years) when revenue is highest and discounting is minimal. The slope gradually flattens as revenue declines and discounting intensifies. By year ten, you’re adding only $119K in present value despite $308K in nominal revenue.
This curve has strategic implications. Most customer value is realized early in the relationship. The first three years generate $1.33 million (51% of total CLV). The last three years generate only $498K (19% of total CLV). This front-loaded value structure argues for aggressive early retention efforts. Losing a customer after year one forfeits much more value than losing them after year seven.
Segment-Specific Lifetime Values
Average CLV per customer is useful for overall valuation, but strategic decisions require segment-level detail. How much is an active high value customer worth versus an active low value customer? The difference guides retention investment:
# Calculate segment-specific CLV
segment_clv = revenue_projection.multiply(discount_factors, axis=1).sum(axis=1) / segment_projection[2015]
segment_clv = segment_clv.replace([np.inf, -np.inf], 0) # Handle divide by zero
# Create comprehensive segment analysis
segment_analysis = pd.DataFrame({
'2015_count': segment_projection[2015],
'avg_2015_revenue': revenue_vector,
'total_segment_clv': revenue_projection.multiply(discount_factors, axis=1).sum(axis=1),
'clv_per_customer': segment_clv
}).round(2)
segment_analysis['pct_of_total_clv'] = (
segment_analysis['total_segment_clv'] / segment_analysis['total_segment_clv'].sum() * 100
).round(1)
print("\nSegment-Level CLV Analysis:")
print(tabulate(segment_analysis, headers='keys', tablefmt='psql'))
Segment-Level CLV Analysis:
+-------------------+--------------+---------------------+---------------------+---------------------+---------------------+
| segment | 2015_count | avg_2015_revenue | total_segment_clv | clv_per_customer | pct_of_total_clv |
+-------------------+--------------+---------------------+---------------------+---------------------+---------------------+
| inactive | 9158.00 | 0.00 | 0.00 | 0.00 | 0.0 |
| cold | 1903.00 | 0.00 | 0.00 | 0.00 | 0.0 |
| warm high value | 119.00 | 0.00 | 43842.90 | 368.43 | 1.7 |
| warm low value | 901.00 | 0.00 | 40766.61 | 45.25 | 1.5 |
| new warm | 938.00 | 0.00 | 0.00 | 0.00 | 0.0 |
| active high value | 573.00 | 323.57 | 1800952.04 | 3143.55 | 68.5 |
| active low value | 3313.00 | 52.31 | 675964.03 | 204.02 | 25.7 |
| new active | 1512.00 | 79.17 | 68563.39 | 45.34 | 2.6 |
+-------------------+--------------+---------------------+---------------------+---------------------+---------------------+
The segment analysis reveals dramatic CLV differences. Active high value customers average $3,144 in lifetime value. Active low value customers average $204. The ratio is 15:1, meaning one active high value customer equals fifteen active low value customers in present value terms.
Even more striking: the 573 active high value customers (3% of the base) generate $1.8 million in CLV (68.5% of total value). The 3,313 active low value customers (18% of the base) generate $676K (25.7% of value). These 3,886 active customers together represent 21% of the customer base but generate 94% of all value.
The inactive, cold, and new warm segments contribute zero CLV because they don’t generate future revenue in our projections (inactive and cold don’t purchase, new warm immediately transition to other segments). The warm segments contribute modestly because customers transition through them briefly on their way to other states.
These numbers have immediate practical implications:
Retention investment: Losing an active high value customer forfeits $3,144 in CLV. You can economically justify spending hundreds of dollars on personalized retention for these customers. Losing an active low value customer forfeits $204, suggesting automated retention campaigns with minimal cost.
Win-back campaigns: Reactivating a high-value customer creates much more value than reactivating a low-value customer. Win-back resources should focus on customers who were previously in high-value segments, not those who were always marginal.
Acquisition targeting: If you can identify prospect characteristics that predict high-value segments, pay more to acquire those prospects. Customers who will become active high value are worth 15x more than typical customers.
Product development: Prioritize features that active high value customers want. Their preferences matter 15x more than low-value customer preferences when making resource allocation decisions.
Business Applications and Strategic Insights
CLV analysis transforms from academic exercise to business tool when you apply it to real decisions. Let’s work through several scenarios:
Scenario 1: Acquisition Campaign Evaluation
Suppose you’re evaluating two customer acquisition strategies:
Strategy A (Aggressive Discount): Offer 40% off first purchase. Expected to acquire 1,000 customers at $150 cost per acquisition. Historical data shows discount-driven customers typically become active low value (average CLV: $204).
Strategy B (Targeted Premium): No discount, but target high-intent prospects with premium messaging. Expected to acquire 300 customers at $200 cost per acquisition. Historical data shows these customers typically become active high value (average CLV: $3,144).
Which strategy is better?
Strategy A: 1,000 customers × $204 CLV = $204,000 total lifetime value. Acquisition cost: 1,000 × $150 = $150,000. Net value: $54,000. ROI: 36%.
Strategy B: 300 customers × $3,144 CLV = $943,200 total lifetime value. Acquisition cost: 300 × $200 = $60,000. Net value: $883,200. ROI: 1,472%.
Strategy B is dramatically superior despite acquiring fewer customers at higher unit cost. CLV analysis reveals this because it captures the long-term value difference between customer types.
Scenario 2: Retention Investment
You have budget for a retention program. Should you target active high value customers (who have high retention rates already) or active low value customers (who have lower retention rates but more room for improvement)?
From our transition matrix, active high value customers have a 74.5% probability of staying in that segment. The 25.5% who leave transition to warm high value. Very few become inactive quickly.
Active low value customers have a 69.3% probability of staying active low value. The remaining 30.7% are more volatile, with some becoming inactive.
Suppose a retention campaign can improve retention rates by 10 percentage points (e.g., 74.5% → 84.5% for high value customers). What’s the value of this improvement?
For active high value: Retaining 10% more of 573 customers saves 57 customers × $3,144 CLV = $179,208 in value.
For active low value: Retaining 10% more of 3,313 customers saves 331 customers × $204 CLV = $67,524 in value.
Even though the low-value segment has more customers who might defect, the high-value segment generates 2.7x more value from the same percentage improvement. Retention investment should focus on high-value customers first.
Scenario 3: Product Line Decisions
You’re deciding whether to launch a premium product line. Development costs $500,000. Market research suggests it will appeal primarily to active high value customers, potentially increasing their average annual spending from $324 to $400.
Is this worthwhile?
The 573 active high value customers generate $1.8M in total CLV currently. Increasing their annual revenue by 23% ($76/$324) would increase their CLV proportionally to $2.22M. The incremental value is $420,000.
But we need to discount this incremental value since it accrues over ten years. If the revenue increase starts immediately and continues, the present value is approximately $350,000 (accounting for the fact that later years’ increases are worth less).
At $350,000 in incremental CLV versus $500,000 in development costs, the project has negative NPV. You’d need the product to either increase spending more than 23% or attract additional high-value customers to justify the investment.
Model Limitations and Assumptions
Our CLV model relies on several assumptions that may not hold perfectly in practice:
Stationary transition probabilities: We assume the 2014→2015 transition matrix stays constant over ten years. In reality, competitive dynamics shift, products evolve, and customer behavior changes. Transition matrices should be updated periodically as new data arrives. A matrix from 2014 probably doesn’t accurately predict transitions in 2024.
No customer acquisition: We model only the existing customer base. Real businesses continuously acquire new customers. A complete CLV framework would model both existing customer evolution and new customer flows. The challenge is that acquisition rates depend on marketing spending, which is a decision variable rather than a forecast.
Segment-based averaging: We assume all customers in a segment have identical CLV. In reality, variation within segments exists. Some active high value customers are more valuable than others. More sophisticated models can incorporate individual-level heterogeneity using techniques like BG/NBD or Pareto/NBD models.
No intervention effects: Our projections assume you take no action to improve retention or increase customer value. Real strategy involves interventions. CLV analysis should guide those interventions by identifying where they create most value, but the projections themselves don’t capture intervention effects.
Discount rate uncertainty: We used 10% as a discount rate. Different rates produce different CLV estimates. At 5%, our total CLV would be higher. At 15%, it would be lower. Sensitivity analysis using multiple discount rates provides a range of estimates rather than a point estimate.
Revenue stability: We assume segment-level average revenues stay constant at 2015 levels. Inflation, price changes, and economic conditions all affect revenue. More sophisticated models might project revenue growth or decline within segments.
Despite these limitations, the model provides valuable strategic insights. Perfect accuracy isn’t the goal. The goal is directing resources toward high-value customers and understanding the economic drivers of customer relationships. Even a rough CLV estimate beats no estimate at all.
From Segments to Strategy: Completing the Journey
We’ve now completed a comprehensive four-part journey through customer analytics:
Tutorial 1 taught us to discover natural customer groupings through hierarchical clustering. We learned that data-driven segmentation reveals patterns human judgment might miss. The exploratory approach identifies segments, but doesn’t prescribe them.
Tutorial 2 showed us how to implement business logic directly through managerial segmentation. We learned that simple rules, informed by domain expertise, often work better operationally than complex algorithms. Transparency and maintainability matter as much as statistical sophistication.
Tutorial 3 introduced predictive modeling to forecast next-period behavior. We built separate models for purchase probability and purchase amount, validated them retrospectively, and combined them into customer scores. This moved us from describing customers to predicting their next moves.
Tutorial 4 extended prediction from single periods to multi-year horizons. We used Markov chain transition matrices to project customer segment evolution over time. By converting projections to revenue and applying discounting, we calculated Customer Lifetime Value, the ultimate metric that quantifies customer relationships financially.
The complete framework now provides:
- Descriptive analytics to understand current customer composition
- Prescriptive analytics to segment customers for operational campaigns
- Predictive analytics to forecast near-term customer behavior
- Financial analytics to value customer relationships over time
This integrated approach supports decisions at every level. Tactical campaign targeting uses predictive scores. Strategic resource allocation uses CLV. Performance monitoring uses actual-to-predicted comparisons. Investment decisions use CLV to justify spending.
The power isn’t in any single technique but in how they work together. Segmentation creates the groups. Prediction identifies high-probability opportunities. CLV quantifies long-term value. Each layer adds insight that guides better decisions.
Conclusion
Customer Lifetime Value represents the culmination of customer analytics. It answers the ultimate question every business faces: what is this customer relationship worth? By projecting segment evolution through Markov chains, translating projections to revenue, and discounting to present value, we transform behavioral data into financial metrics executives understand.
Our analysis revealed that the average customer in this database is worth $143 in present value over ten years. But this average masks dramatic variation. Active high value customers are worth $3,144 each. Active low value customers are worth $204 each. The 15:1 ratio means customer selection and retention have enormous financial leverage.
The projections also revealed the natural erosion of customer value over time. Without acquisition and retention initiatives, revenue declines 36% over ten years as customers naturally churn. Maintaining revenue requires continuous effort. CLV analysis quantifies exactly how much effort is economically justified for different customer types.
The framework we’ve built throughout this series balances statistical rigor with business practicality. We didn’t use the fanciest algorithms or most complex models. We used approaches that work with available data, produce interpretable results, and integrate into operational systems. Logistic regression, ordinary least squares, RFM segmentation, transition matrices. These aren’t exotic techniques requiring PhD-level expertise. They’re workhorse methods that deliver results.
The most important lesson isn’t technical. It’s strategic. Customer analytics is valuable only when it changes decisions. Segmentation is valuable when it guides targeting. Prediction is valuable when it prioritizes investments. CLV is valuable when it determines spending limits and resource allocation. The goal is better decisions, not sophisticated models.
Start simple. Segment your customers using basic RFM analysis. Calculate segment-level revenue. Build simple transition matrices from year-to-year data. Estimate CLV even if roughly. Use these estimates to guide a few decisions. Measure results. Refine your approach. Iterate.
The businesses that win at customer analytics aren’t necessarily those with the best data scientists or biggest budgets. They’re the ones who systematically use customer insights to guide decisions, measure outcomes, and improve continuously. That discipline matters more than any specific technique.
You now have the complete toolkit to value your customer base, segment it strategically, predict future behavior, and allocate resources rationally. The techniques work. The question is whether you’ll use them to transform how your organization thinks about customers. That’s not a technical challenge. It’s a leadership challenge.
Go make better decisions.
References
-
Lilien, Gary L, Arvind Rangaswamy, and Arnaud De Bruyn. 2017. Principles of Marketing Engineering and Analytics. State College, PA: DecisionPro.
-
Fader, Peter S., and Bruce G. S. Hardie. 2009. “Probability Models for Customer-Base Analysis.” Journal of Interactive Marketing 23 (1): 61-69.
-
Pfeifer, Phillip E., and Robert L. Carraway. 2000. “Modeling Customer Relationships as Markov Chains.” Journal of Interactive Marketing 14 (2): 43-55.
-
Netzer, Oded, and James M. Lattin. 2008. “A Hidden Markov Model of Customer Relationship Dynamics.” Marketing Science 27 (2): 185-204.
-
Grönroos, Christian. 1991. “The Marketing Strategy Continuum: Towards a Marketing Concept for the 1990s.” Management Decision 29 (1). https://doi.org/10.1108/00251749110139106.
-
Gupta, Sunil, Donald R. Lehmann, and Jennifer Ames Stuart. 2004. “Valuing Customers.” Journal of Marketing Research 41 (1): 7-18.
-
Arnaud De Bruyn. Foundations of Marketing Analytics (MOOC). Coursera.
-
Dataset from Github repo. Accessed 15 December 2021.
Business Analytics Tutorial 